Monthly Archives: December 2023

ARM47 ir PID dalis #4

O dabar pašnekėsim apie STM32F4 serijos variantą ir source code. Pirmiausia- kodėl 4 serija? Todėl, kad tokia PCB pasitaikė po ranka. Ir tikrai ne dėl kažkokio mistinio FPU ar net DSP. Ir dar neaišku, ar mano turimas MCU yra originalas, o ne koks nors permarkiruotas šlamštas. Šaltinis solidus, bet kodėl jie juos išmetė? Reikia surasti kur nors panaudotą procesorių ir palyginti.

Source code yra sugeneruotas su CubeMX programa, kompiliuota su gcc. Ryšiai su kubiko paprogramėm tik per callback. Ir tai tik naudojam USB biblioteką (virtualus COM portas) ir taimerių pertraukimus. ADC skaitom blokavimo režime.

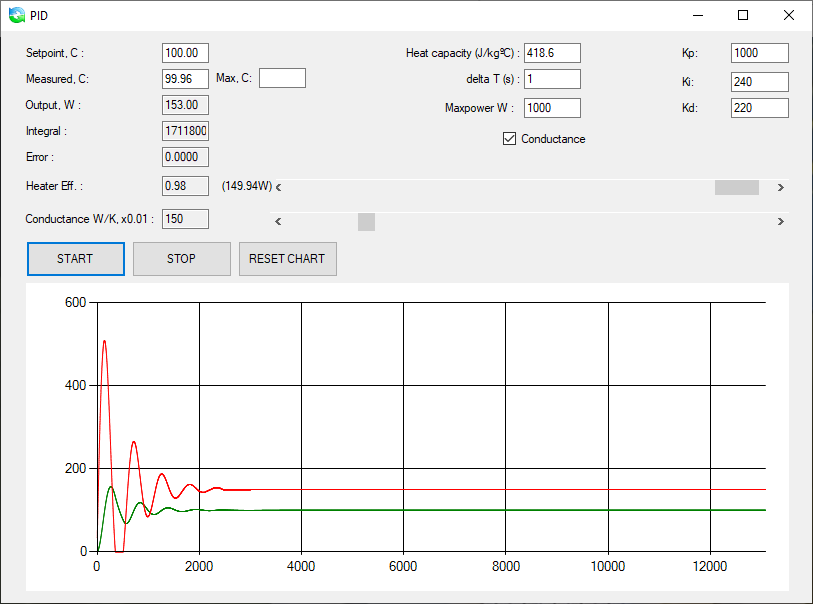
Pats PID skaičiavimas, float variantas visiškai toks pats kaip ir teoriniam variante:

float pid_generic(float measured, float setpoint, float amplif)
{
float output;
float deritative;
float error;
float proportional;
 
error = (setpoint - measured)/10;
proportional = error;
 
integral=integral + error * pid_dt;
deritative = (error - old_error) / pid_dt;
old_error = error;
 
output = (PID_KP * proportional + PID_KI * integral + PID_KD * deritative) * amplif;
 
return output;
}

Atsirado papildomas parametras “amplif” – tai bendro rezultato daugiklis, kaip ir sustiprinimas (ar susilpninimas). Teoriškai tą patį galima atlikti su pagrindiniais parametrais (P, I, D), bet taip lengviau priderinti prie “krosnelės” galingumo: kaitinimas dirba su integer skaičiais, ir PID rezultatas apsiapvalina. Taip prarandam “jautrumą”. Ir dar temperatūros parodymus pasmulkinam- tik dėl koeficientų.

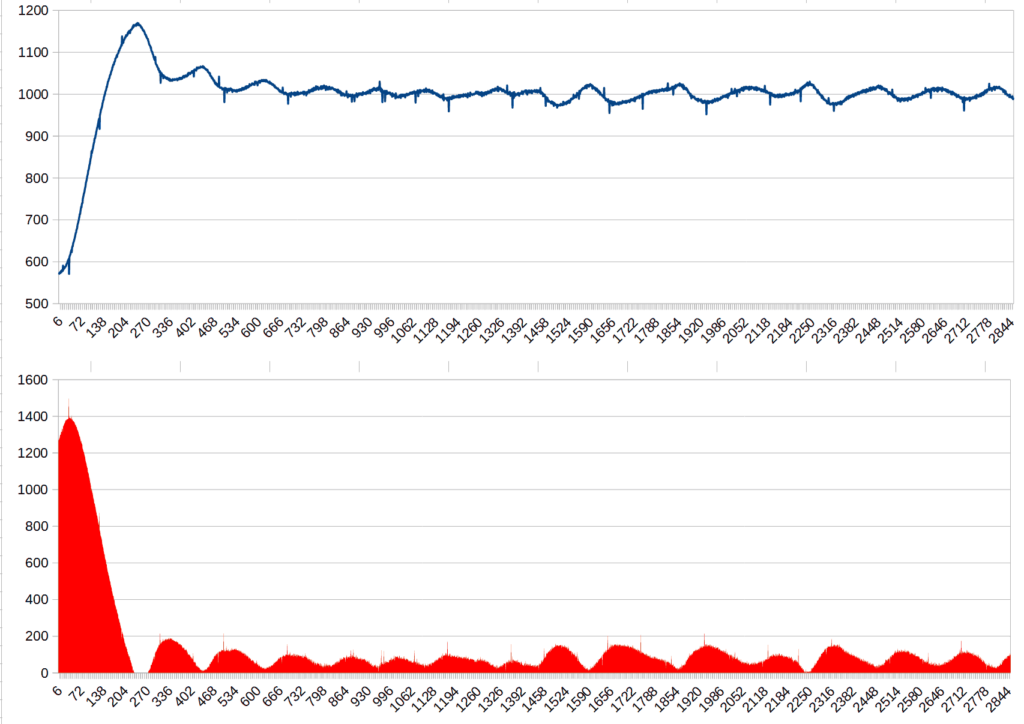
uint32_t CalcTemp(void)
{
uint32_t a;
a=median_filter(adc_read_blocking(ADC_CHANNEL_4));
a=median_filter(adc_read_blocking(ADC_CHANNEL_4));
//a=median_filter(adc_read_blocking(ADC_CHANNEL_4));
// 786 - max t, 0.62V ->1655
// 3529 - kambario t, 2.83V -> 283
return (4096-a)/2; //12 bitų max apverčiam ir pašalinam LSB.
}
 

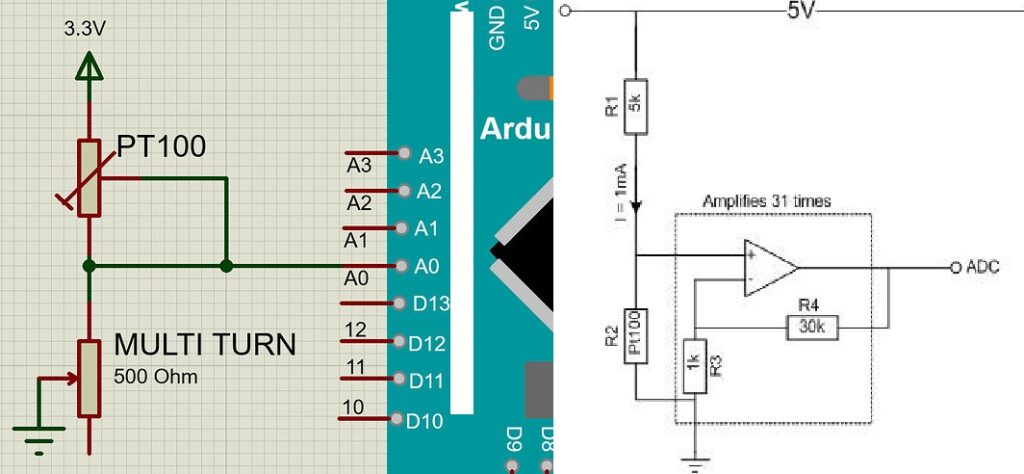
Dėl ADC blogumo, matuojam kelis kartus, invertuojam (dėl schemotechnikos išėjimas mažėja didėjant temperatūrai) ir pašalinam mažiausią bitą, nes jis rodo kvailystes. Funkcija “median filter” vogta iš interneto. Tai funkcija, kuri teoriškai turi išfiltruoti sporadiškus nukrypimus: jei eina 5, 6, 4, 3, 100 – tai tas šimtas kaip ir ne į temą. Kiek veikia per daug netikrinau. Manau, reikia dar padidinti buferį.

  1. readtemp=CalcTemp();
  2. pwm=PID(readtemp, SETTEMP);
  3. SetPWM(pwm);

O čia pats pagrindinis ciklas, kuris kartojamas sistemingai: 1 – nuskaitom, 2 – paskaičiuojam. 3 – valdom kaitinimą.

Visas likęs source kodas aptarnauja kontrolerio valdymą per terminalą (galima keisti parametrus) ir duomenų išmetimą analizei. Tai tik eksperimentinis variantas- darbiniam trūksta dar visokių apsaugų, normalaus valdymo ir indikacijos. Ir aišku, išėjimas čia PWM, kad tinkama mažam rezistoriui, bet ne tikram šildytuvui. Dar nesugalvojau, kaip padaryti korektiškai proporcinį valdymą realiai rėlei ar 50Hz simistoriniam reguliatoriui. Jei užteks kantrybės, tema bus vystoma.

Pats pilnas STM32F446 PID controller source code skirtas gcc ir kartu CubeMX projekto failas (versija užrakinta posto datai, galimi patobulinimai). Prie papildų- median filter, ftoa ir usb paprogramės. Visa mano kūryba “USER” aplanke.

PID, dalis #3, FLOAT ir STM32F4

Dabar, apjungiant senesnius straipsnius [0, 1, 2], sumontavau kažką panašaus į PID termokontrolerį.

PID controller STM32F4xx

Ant lentos surinkta mano universali White Pill plokštė, tik su STM32F446 procesorium (toks biški itartinas tas procesoriukas, kažko man taimeriai neteisingai veikia). Dešinėje- mano Pt100 termorezistoriaus stiprintuvas. Geltona plokštė, tai kiek pasvilęs RGB LED “stiprintuvas”- galvaniškai atrišti trys galingi MOSFET valdomi per optoporas. Optoporų rezistorių teko sumažinti, kad nuo 3V procesoriuko pilnai valdytusi. O vienas “RGB LED stiprintuvo” kanalų paprasčiausiai valdo vielinį rezistorių kairėje, į kurį įkištas Pt100 jutiklis- tai mikro krosnelė, kurioje bandysim stabilizuoti temperatūrą.

Šiame eksperimente naudojamas source code su “float” kintamaisiais. Nenorėjau iškarto eksperimentuoti su integer matematika, nes dar nežinojau savo “krosnelės” parametrų.

PID įėjimas- ADC, išėjimas PWM. Panaudojau “prabangų”, 16 bitų PWM, nes norėjau platesnio reguliavimo. O su ADC išėjo biški problematiškai- STM32F446 ADC biški gaidiškas (net jo datašytas tai rašo). Nėra jokio tikslumo ir rezultatai vaikšto. Todėl panaudojau matematinį “filtrą” ir kelis nuskaitymus iš karto. Temperatūra matuojama “papūgomis”1 – 1000 vienetų tai kažkur 40℃, o apie 280 tai kažkur kambario. Užduotis- palaikyti 1000 vienetų temperatūrą viduje rezistoriaus.

Pagrindinė bėda- tiek rezistorius, tiek Pt100 žiauriai lėtai veikia. Todėl teko gana ilgai žaisti su koeficientais, ir dar iki optimalumo jie neprivesti.

PID chart

Mėlynas grafikas- rezistoriaus temperatūra. Raudonas grafikas PWM užpildymas. Matosi periodiniai triukšmai tiek temperatūros nuskaityme, tiek išeinančiam signale. Reikia rimtesnio skaitmeninio filtro. Dar kiek palaikius, paskutinius 400+ skaitymų temperatūros vidurkis buvo lygiai 1000 papūgų. Tačiau signalas nesusistabilizavo. Gal per maža PWM reikšmė:

PID PWM

Vos 2% iš viso. Gal vėliau pabandysiu su aukštesne temperatūra. (PWM signalas iš MOSFETO- žemas lygis reiškia, kad rezistorius prijungtas prie žemės ir kaista). Beja, gal ir siauresnis signalas per siauras šiems kiniškiems mosfetams. Pastebėjau, kad prie mažesnių signalų, PWM dingsta iš oscilografo ekrano.

Pratesimas ir veikiantis source code sekančiam straipsnyje.

  1. Tai santykinis matvimo vienetas iš seno multifilmo, kai matavo smauglio ilgį. ↩︎

Pt100 nuskaitymas

PT100 tai termorezistorius, kuris gana tiksliai matuoja temperatūrą. Skaičius 100 sako, kad prie 0℃ rezistoriaus varža yra 100Ω. O raidelės Pt sako, kad pirmieji šio rezistoriaus variantai buvo padaryti iš platinos. Ar dabar ten yra tos platinos aš jau nežinau. Bet seni tarybiniai termorezistoriai viduje turi labai labai plonos platinos vielos. Keičiantis temperatūrai keičiasi ir tos vielos varža.

O kaip nuskaityti tuos varžos omus? Pirmi pasiguglinimai parodo:

schemos

Čia visdėlto blogos schemos… Schema kairėje, jungimas prie mano nemėgiamo arduino. Paduodam elektrą per rezistorių ir matuojam su ADC parodymus. Atrodo kad viskas paprasta? Bet neteisinga- pirmiausia, per Pt100 rekomenduojama srovė iki 1mA. Čia 5.5mA ir pats termistorius jau nuo srovės kaista. Antroje schemoje srovė jau pamažinta ir kad ADC kažką matytu, pastatytas operacinis stiprintuvas (su 31 karto stiprinimu). Kaip ir logiška, bet deja, ne. Pt100 termistoriaus varža kinta tik keliasdešimt omų: prie 100℃ jis 138.5. Matuojant nuo 0℃ iki 100℃ turim tik 38.5Ω pokytį.

Ir dar abi schemos turi kitą problemą:

Paskaičiuojam schemą kairėje: įtampos pokytis ADC kojoje nuo 2.75V iki 2.58V, apie 0.1658V visam šimtui laipsnių. Kad ir koks geras ADC, didžioji jo matavimo dalis bus nenaudojama, o ir rezoliucija nebus labai jau didelė.

Antra schema, atrodo kaip ir geresnė, bet čia ta pati bėda- net po sustiprinimo, darbinis diapazonas nuo 3.04V iki 4.18V, apie 1.14V šimtui laipsnių. Kodėl, o todėl, kad pastovioji dedamoji nuo didžiosios dalies varžos irgi “pasidaugina” su operacinius stiprintuvu.

Ką daryti? Ogi daryti naudojant daugiau rezistorių:

pt100 amplifier

Šis testinis chaosas tai instrumentinis operacinis stiprintuvas LT1167 ir “matavimo tiltas” (Wheatstone bridge) – viršuje, kairėje. Papildomi rezistoriai dar padaro taip, kad diferencinis signalas gautusi virš 2.5V nuo žemės- čia jau LT1167 veikimo specifika naudojant vienpoliarį maitinimą. Dar, išėjimo signalas žemiau 0.6V nenusileidžia- čia irgi specifika, nėra jis rail-to-rail. Naudojant dvipoliarį maitinimą, tokios nesąmonės visiškai nereikalingos.

Šis “tiltas” duoda vieną triuką- taip galima iš schemos magiškai pašalinti “nenaudojamus” omus. Mano tiltas buvo surinktas iš trijų 120Ω rezistorių ir Pt100 termorezistoriaus. Dabar operacinis (čia instrumentinis) stiprintuvas gali žymiai daugiau stiprinti signalą. Testinėje schemoje gavosi kažkur nuo 6V iki 0.6V keičiant temperatūrą nuo kambario (~23℃) iki kažko karšto, bet ne verdančio. Maitinimas rodos buvo nuo 15V vienpoliario, o srovė per Pt100 ribota kažkur 10kΩ varža. (Tai tik testinė plokštė, neskirta naudoti su tikru procesorium).

Dar reikia sukonstruoti tikrą stabilizuotą maitinimo šaltinį (gal su specialia mikroschema) ir galimą viską sumontuoti gražiai. Bet tikslas tikrai nėra toks, tai tik tarpinis straipsniukas prie PID kontrolerio eksperimento.

PID, dalis #2, o kodėl FLOAT?

Jei norėčiau perkelti seniau aprašytus algoritmus į kokį mikrokontrolerį, viskas lengvai nusikopijuotu. Juk šiuolaikinis gcc puikiausiai palaiko slankiojo kablelio matematiką (float). Tačiau float yra lėtai ir užima daug vietos. Ypač dalyba. Net naudojant integer matematiką, dalyba yra toks nerekomenduojamas reikalas.

Ar tikrai reikia dalybos? Prisimenam formulę:

PID

Čia dalyba yra tik pačioje dešinėje, kur dalinasi iš dt. O jei pas mumi dt = 1? Kas sako, kad reikia skaičiuoti realiom sekundėm? Kas draudžia skaičiuoti kokiais nors išgalvotais, santykiniais vienetais. O jei tikrai reikia, kas draudžia funkciją skaičiuoti kitokiu dažniu. Išpaprastinam dt.

O dabar ar tikrai reikia float? Kas trugdo skaičiuoti viską integer? Gal koeficientai Kp, Ki, Kd? O kas trugdo juos padidinti šimtus kartų? Niekas. O kodėl šimtus? O kodėl ne 256 kartus? Ar 2^15 kartų? Svarbu, kad tik rezultatas tilptu į procesoriuko integer talpą. Viską skaičiuojam dideliais skaičiais ir jau galutinį rezultatą vėl sumažinam kažkiek kartų. Svarbu tik atburti koeficientus.

Čia visiškai ta pati programa, tik pats PID kontroleris veikia su 64 bitų integer matematika. O delta T yra vienetas. (Šildymo modelis tebeveikia su float matematika). Aišku čia kiek nepataikiau su koeficientais ir sunkiai susistabilizavo. Bet veikia!

    Private Sub DoPID()
        Dim P_error As Int64
        Dim P_proportional As Int64
        Dim P_deritative As Int64
 
        Dim sp As Int64 = CInt(setpoint) << 16
        Dim m As Int64 = CInt(measured) << 16
 
        P_error = sp - m
        P_proportional = P_error
        P_integral = P_integral + P_error * pid_dt
        P_deritative = (P_error - P_previous_error) / pid_dt
        output = (pid_kp * P_proportional + pid_ki * P_integral + pid_kd * P_deritative) >> 28
        If output > outmax Then output = outmax
        If output < 0 Then output = 0
        P_previous_error = P_error
    End Sub

Dar kiek pažaisiu su bitais ir koeficientais. Bus daugiau.

PID, dalis #1

Teorija aišku. Kaip ir visi “interneto puslapiai” turiu įdėti šią formulę vogta iš vikipedijos…

PID

Tačiau tai paprasti puslapiai- mano “brain dump” t.y. čia bus neteisingas paaiškinimas kaip aš supratau.

Formulę susideda iš trijų dalių: prie Kp, Ki ir Kd.

Kp, tai proporcingas skaičius nuo klaidos. Išmatuojam sakysim temperatūrą, palyginam su reikiama, gaunam skirtumą ir jį naudojam rezultatui. Pats koeficientas Kp tai tik ant kiek jautriai reaguojam. Gaunasi- per šaltas, dar padidinam liepsną po puodu. Kuo skirtumas (klaida) mažesnė, tuo mažiau įtakoja. Gaunasi matematinis paradoksas, kad niekada nesigaus tiksli temperatūra. Aišku realiam pasaulyje dėl apvalinimo ir matavimo tikslumo, rezultatas pasiekiamas. Tačiau galimas didelis overšotas (per didelė temperatūra) arba labai lėtai pasiekiamas reikiamas rezultatas.

Ki, tai integralinė dalis. Čia kaupiasi klaida. Klaida turi ženklą (per karštá, per šaltá), o kai viskas gerai, tai klaida turi nusinulinti. Jei dėl kažkokių nors priežasčių tai nepavyksta, tai “likutinė” susikaupusi klaida priveda rezultatą prie teisybės. Įtariu, kad šita dalis “amortizuoja” reakciją.
Mano matematiniam modelyje, kai sistema stabilizuojasi, “integralo” reikšmė rodo mano teorinio šildytuvo išskirta energiją: (0.98 naudingumas, o integralas – 102. Čia 10.2W išskiriama energija, o 10W atšalimas). Čia kaip ir sistemos nuostoliai. Tuo tarpu Kp dalis jau nulinė, nes nebėra temperatūros skirtumo.

Kd, pati mistiškiausia, išvestinė dalis. Paprastai šnekant, tai kokiu greičiu kažkas keičiasi ir pagal tai bandom spėti kas bus ateityje. Kadangi formulė paprasta, tai spėjimas gali ir nepataikyti.

Visų šių parametrų suma ir yra reguliuojamas poveikis. Tačiau čia prasideda tiuninimas su koeficientais: Kp, Ki ir Kd. Visiškai nėra jokių universalių skaičių, kiekviena sistema turi savo skaičius. Žodis sistema reiškia ne tik matematinę formulę, bet ir visus fizinius parametrus ir bėdas: matavimo tikslumus, sistemos inerciją (tiek šildymo, tiek matavimo, tiek šildomo objekto). Yra net keli metodai, kaip koeficientus paskaičiuoti, bet geriausiai stebėti situaciją ir koeficientus pasitiuninti rankiniu metodu. Panaudojus neteisingus (dažniausiai per didelius) koeficientus, sistema gali “siubuoti” t.y. suptis kaip kokios supynės ir niekada nesusistabilizuotis. O per maži skaičiai labai pailgina sistemos reakcijos laiką. (nulinės reikšmės išjungia atitinkamas formulės dalis: taip gaunasi PI ir P kontroleriai.)

Formulė atrodo sudėtinga, bet čia tik dėl mandro užrašymo. Visual Basic kalboje tai viskas paprasčiau:

    Private Sub DoPID()
        P_error = setpoint - measured
        P_proportional = P_error
        P_integral = P_integral + P_error * pid_dt
        P_deritative = (P_error - P_previous_error) / pid_dt
        output = pid_kp * P_proportional + pid_ki * P_integral + pid_kd * P_deritative
        P_previous_error = P_error
    End Sub

Kaip ir viskas. Šią funkciją (paprogramę) reikia paleidinėti pastoviai, teoriškai kas “pid_dt” laiko tarpą. Tačiau tikslūs skaičiai reikalingi tik tada, kai skaičiuojam tikslius vatus ar džiaulius. Jei skaičiuojam santykiniais papūginiais vienetais, tai net “dt” galima išpaprastinti. Ir reikia išsaugoti dvi reikšmes sekančiam skaičiavimui: “P_previous_error” ir kaupiamąjį integralą “P_integral“.

Šiame matematiniam modelyje “output” gali būti ir neigiamas (čia gautusi kaip šaldymas), tačiau realiam pasaulyje šildymo elementas netik negali šaldyti, bet ir jo galingumas ribotas. Todėl programoje naikinam neigiamus skaičius ir ribojam maksimumą. Šie ribojimai visiškai neįtakoja funkcijos rezultato.

Pratesimas – 2 dalis.

PID, dalis #0

Pasišlykštėjęs kiniškų termokontroleriu nutariau kiek pasidomėti PID kontrolerio teorija. O tam reikėjo pasirašyti šildytuvo modelį (emuliatorių).

PID emuliatorius

Gavosi maždaug toks. Tai 100ml vandens kuris neverda (sferinio arklio vakuume) kaitintuvas su stabiliu aušinimu. Man tikrai patiko, kaip kontroleris reaguoja į netikėta aušinimo pastiprinimą ir kaip jis stabilizuojasi.

Kol kas tik tiek. Taip buvo pirmas vakaras. Pratesimas jau čia.